We have studied one degree of freedom planar mechanism. These mechanisms can have N number of links and for each link there will be 3 equilibrium equations, which means 3N equation. Our main objective will be to find the unknown reactions/torques with support from the known. We will use the method of free body diagram to develop the 3N equations and then simultaneously solve it. However, sometimes it may be very cumbersome to solve the equations if the numbers of links are many. We will understand the method by taking some example cases.
Case 1: Slider crank mechanism
This slider-crank mechanism is in static equilibrium in the shown configuration. A known force F acts on the slider block in the direction shown. An unknown torque acts on the crank. Our objective is to determine the magnitude and the direction of this torque in order to keep the system in static equilibrium.
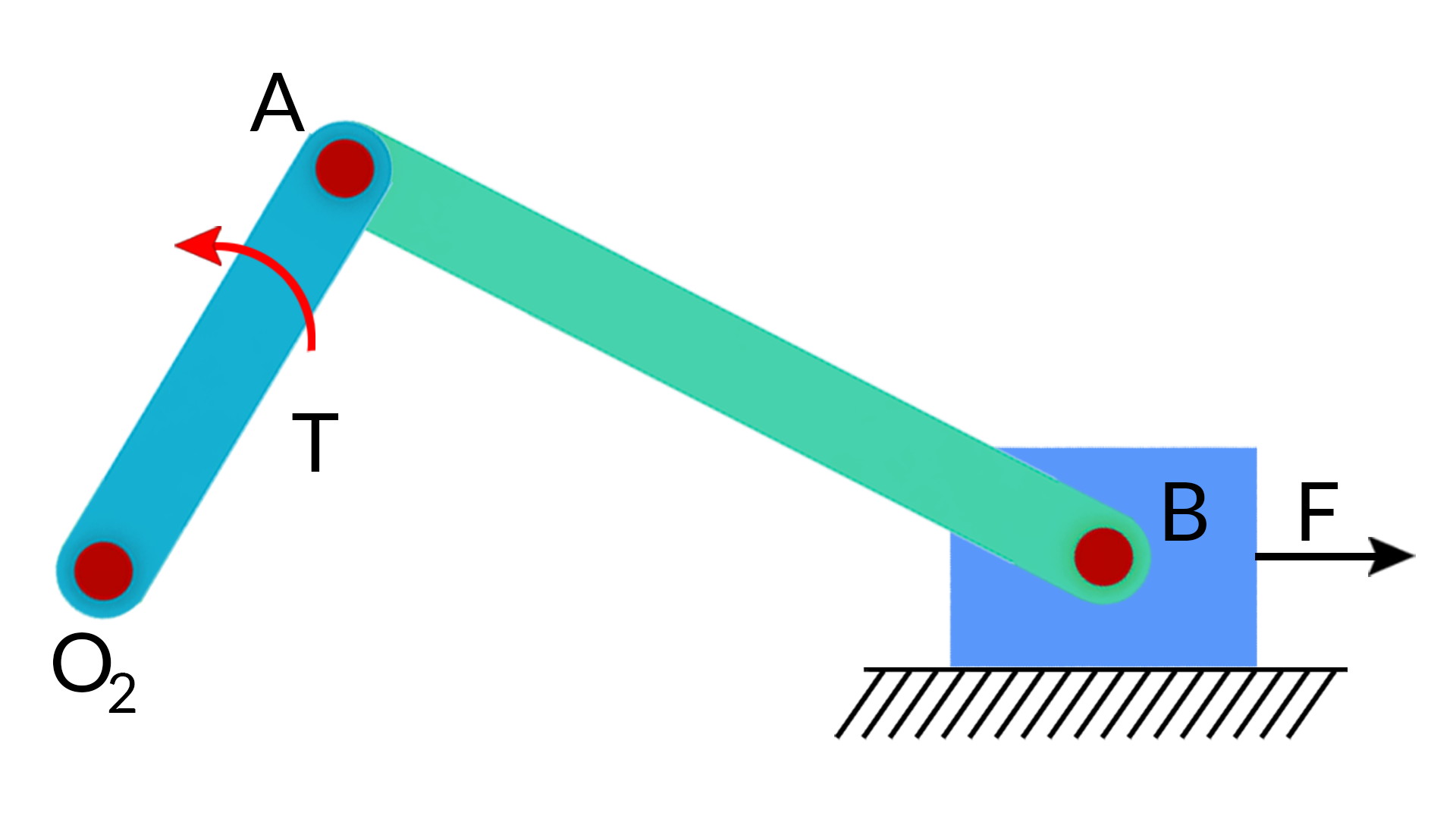
We construct the free body diagrams for each link.
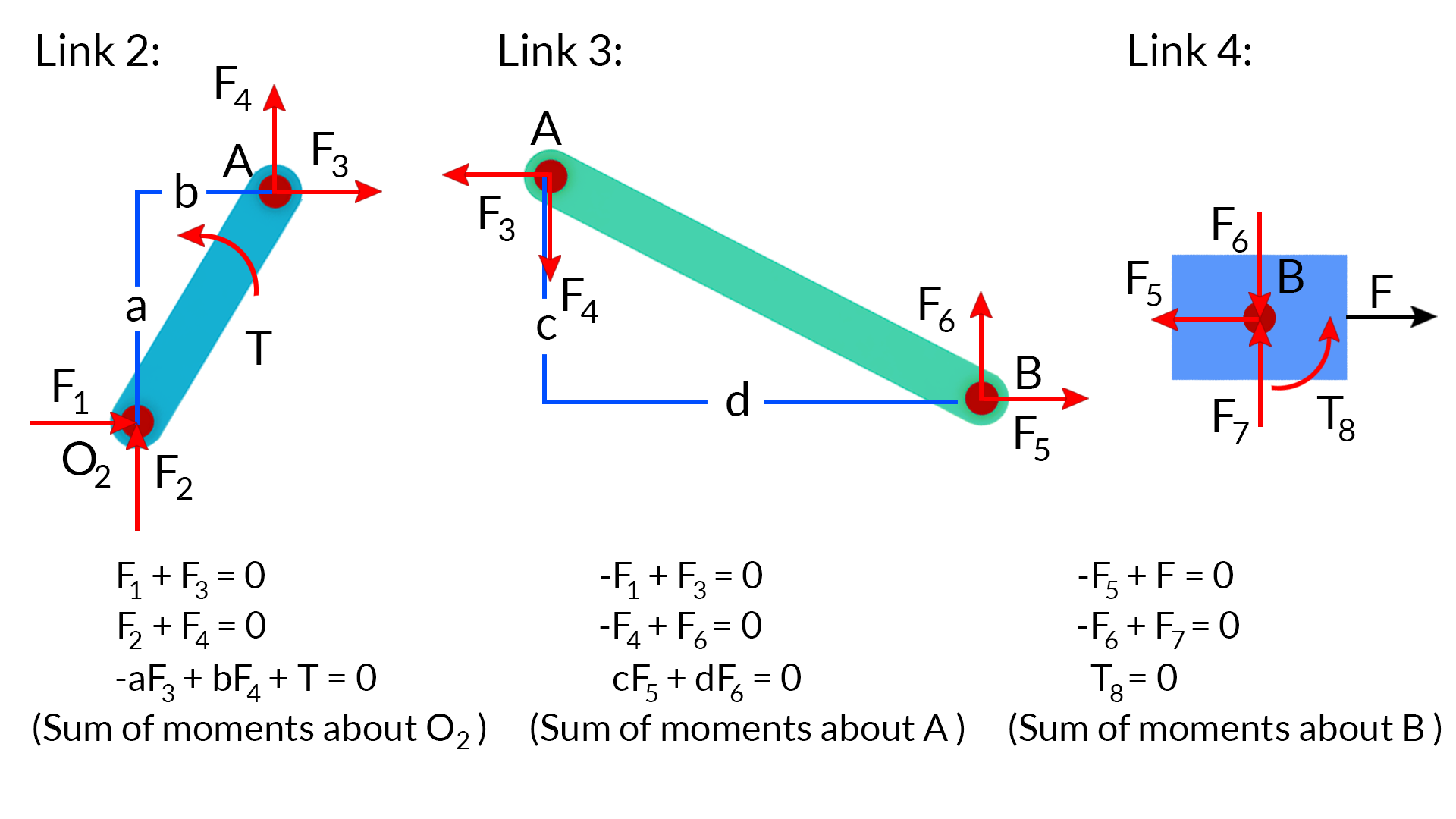
The reaction forces at the pin joints are unknown. Each reaction force is described in term of its x and y components, where the direction of each component is assigned arbitrarily. For notational simplification, simple numbered indices are used for all the components. For each link we construct three equilibrium equations. The moment arms are measured directly from the figure. Note that F7 and T8 are the reaction force and torque due to the sliding joint. These 9 equations can be put into matrix form.
⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜110000000001000000110−a−10000001b0000000001c−10000000d0−10000000010000000001000100000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜F1F2F3F4F5F6F7T8T⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜000000−F00⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
The unknowns and their coefficients are kept on the left-hand side and the only known quantity, the known applied force F is moved to the right-hand side. This set of 9 equations in 9 unknowns can be solved by any preferred numerical method. If the arbitrarily assigned direction to a force component or a torque is not correct, the obtained solution will be a negative quantity.
Case 2: Now in the same question of case 1 let us add the effect of gravity and solve again for the unknowns.
The new free body diagram of the links will be as below
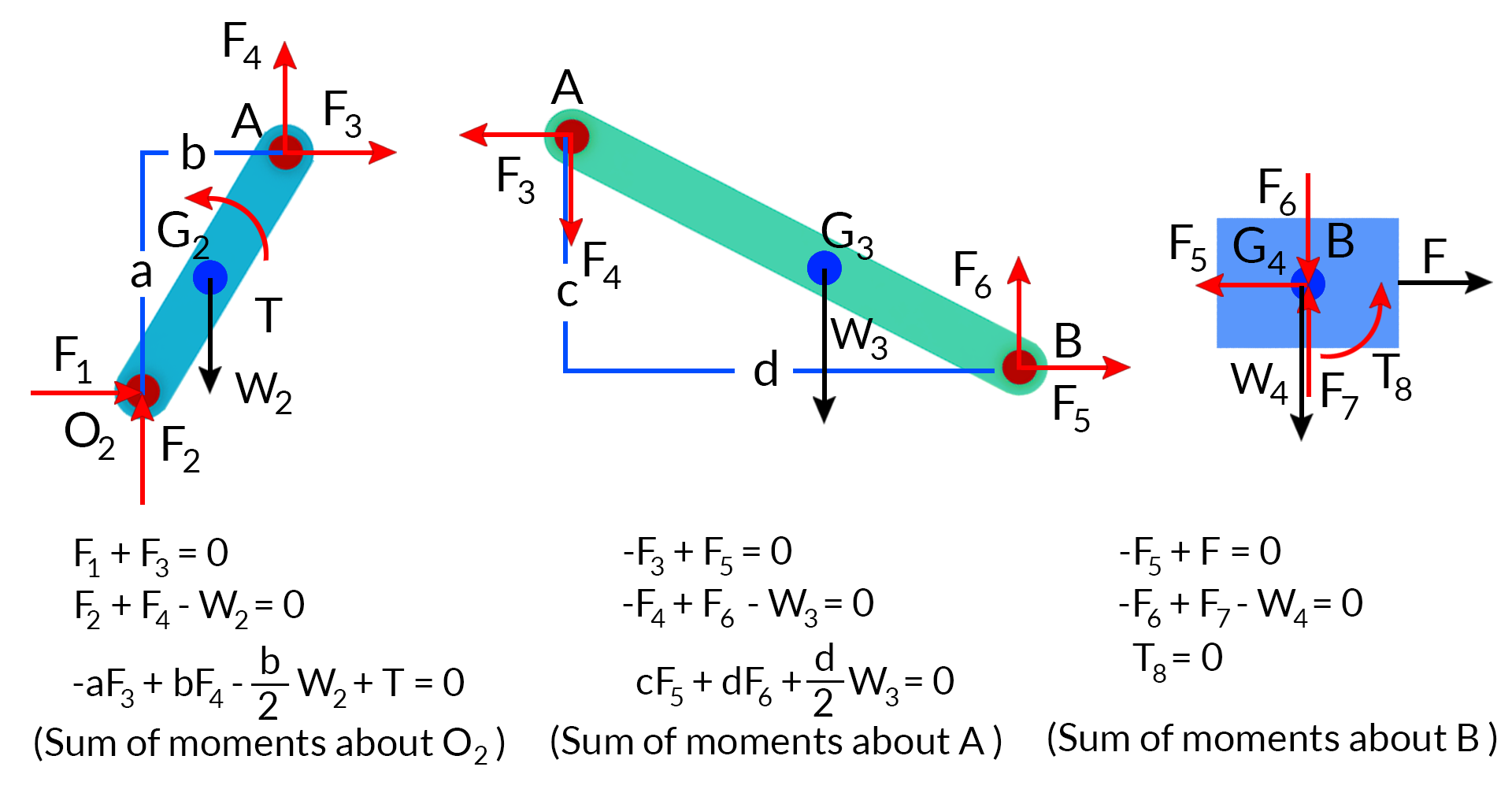
These 9 equations are expressed in matrix form and solved for the 9 unknowns by putting them in the matrix form.
⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜10000000001000000010a−10000001b0−1000000000c−10000001d0−10000000010000000001001000000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜F1F2F3F4F5F6F7T8T⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜0W2bW2/20W3−dW3/2−FW40⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
Case 3:
Let us again solve the case 2 by adding frictional force between the slider and ground.
We see that the FBD of the crank and con rod remains same but the FBD of the slider will change as below
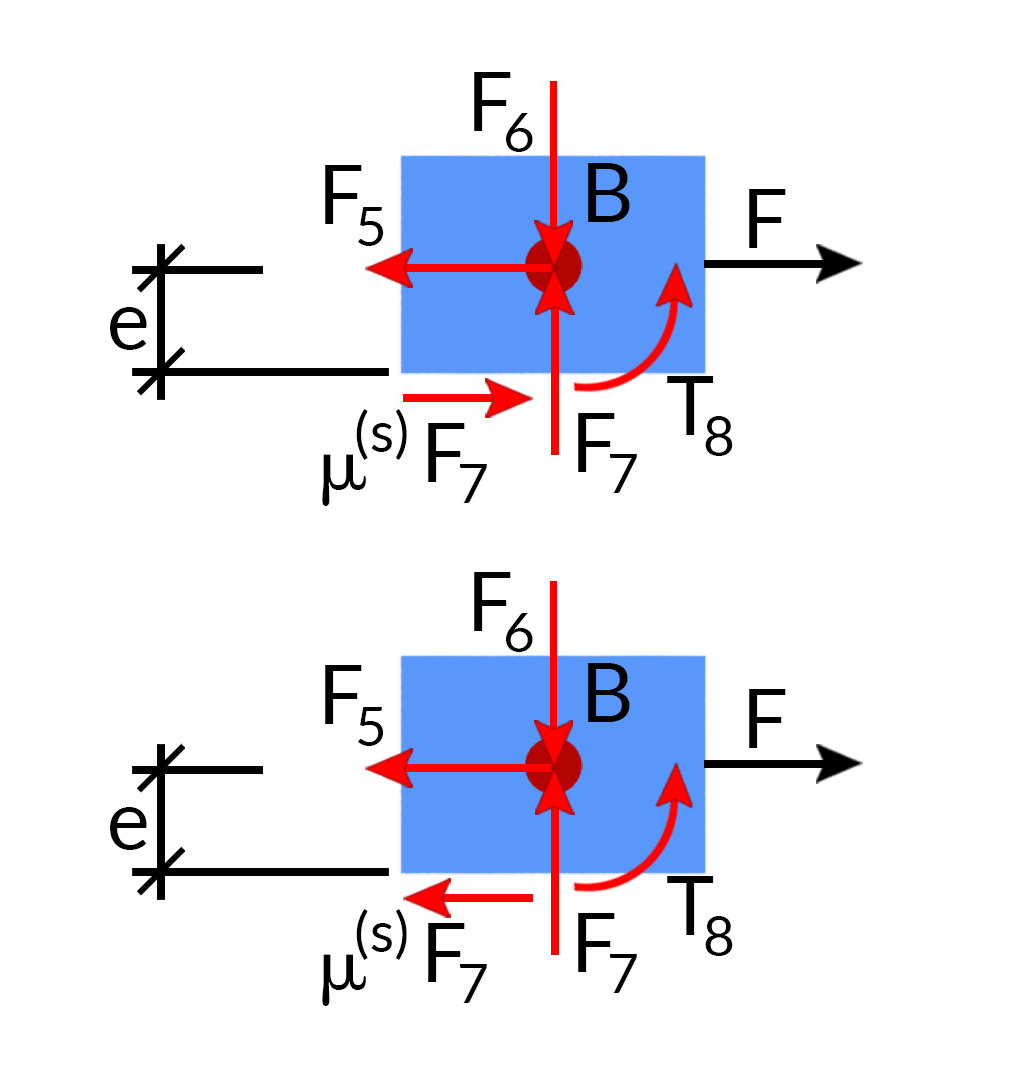
Since frictional force is in the direction against the direction of motion and we are solving for static equilibrium, we will have to take both the cases i.e, when the slider has a tendency to move left and when the slider has a tendency to move right. Corresponding equilibrium equation will also change accordingly
ÀF5+F+Ö(s)F7=0
ÀF6+F7=0 (The block tends to move to the left)
T8+eÖ(s)F7=0
ÀF5+FÀÖ(s)F7=0
ÀF6+F7=0 (The block tends to move to the left)
T8ÀeÖ(s)F7=0
The new matrix of 9 equations will be as below
⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜10000000001000000010−a−10000001b0−1000000010c−10000001d0−10000000±μ(s)1±eμ(s)000000000001000000⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜F1F2F3F4F5F6F7T8T⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜000000F00⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
We construct two complete sets of equations for these two cases. The two sets are presented together as shown. We solve each set of equations twice: once with the positive sign in front of μ(s) and once with the negative sign. Each solution yields a value for the unknown torque, Tleft and Tright . As long as the applied torque stays in the range of Tleft to Tright , the system remains in static equilibrium.