1.1 Belts

Belts are power transmission components. The function of a belt drive is to transfer rotation from one shaft to another, eitherto transfer power, or convey product. The different types of belts available for each purpose shows how adaptable belts are to any industry.

Advantages and disadvantages of Belt drive
Advantages:

1. No lubrication is required.
2. Dampens shock loads.
3. Quieter than chain drives.
4. Low maintenance.
5. Low wear on pulleys so they have long working life.
6. Belts are not expensive to replace.

 

Disadvantages:

 

1. Belts can’t be repaired and length can’t be adjusted.
2. Extreme environmental conditions such as extreme temperatures, high moistureand exposure to chemicals can damage the belts.

1.2 Types of Belts

The flat belt is rectangular in cross-section. All flat belts have a natural tendency to move laterally. Therefore a flat or straight pulley is not recommended, as the belt would walk off the pulley. To keep the belt in the centre of the pulley it must have a crown. The V-belt is trapezoidal in section. It utilizes the force of friction between the inclined sides of the belt and pulley. They are preferred when distance is comparative shorter. Several V-belts can also be used together if power transmitted is more.

The circular belt or rope is circular in cross section. Several ropes also can be used together to transmit more power.

1.3 Belt Drives

1. open belt drive, and
2. cross belt drive.

 1.3.1 Open Belt Drive

Open belt drive is used when drive and driven pulley has to rotate in the same direction. It is desirable to keep the tight side of the belt on the lower side and slack side at the top to increase the angle of contact on the pulleys.

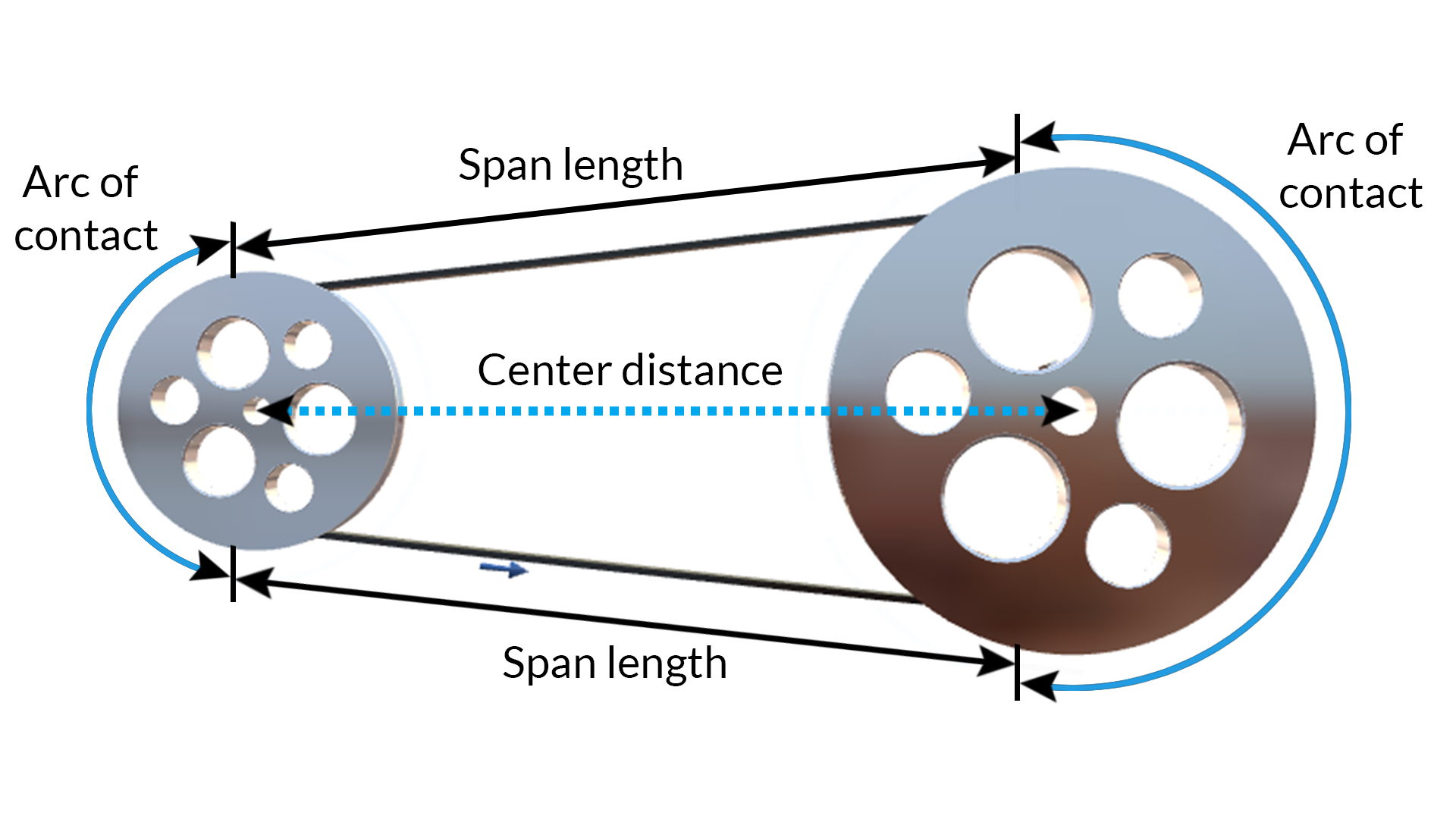
Open Belt Drive (Fig.- 4.1)

The standard terms used in V belt and timing belt drives:

 

1. Driverdrive pulley or motor pulley
2. Drivendriven pulley or final pulley
3. Span length where the belt leaves one pulley and then touches the other pulley.
4. Centre distance the distance between the centre of the pulleys, used for determining the belt length with a calculation
5. Arc of Contact the angle of wrap around each pulley – the bigger the arc of contact is the more power can be transmitted

 1.3.2 Open Belt Drive

In cross belt drive, the pulleys rotate in the opposite direction. The angle of contact of belt on both the pulleys is equal. In this kind of drive the belt has to bend in two different planes. As a result of this, belt wears very fast and therefore, this type of drive is not preferred for power transmission. This can be used for transmission of speed at low power.

1.4 Length of the Belt

The length of the belt is determined by taking a measuring tape and following the path of the belt around all of the pulleys, or through computer aided design (CAD) techniques.

 1.4.1 Open Belt Drive

The open belt drive is shown in the figure. Let O1 and O2 be the pulley centres and AB and CD be the common tangents on the circles representing the two pulleys. The total length of the belt ‘L’ is given by

L = Belt length
C = Centre of pulley shaft to centre of pulley shaft distance
D = pitch diameter of large pulley
d = pitch diameter of small pulley

$\beta$ be the angle subtended by the tengents AB and CD with $O_1O_2$ 

 

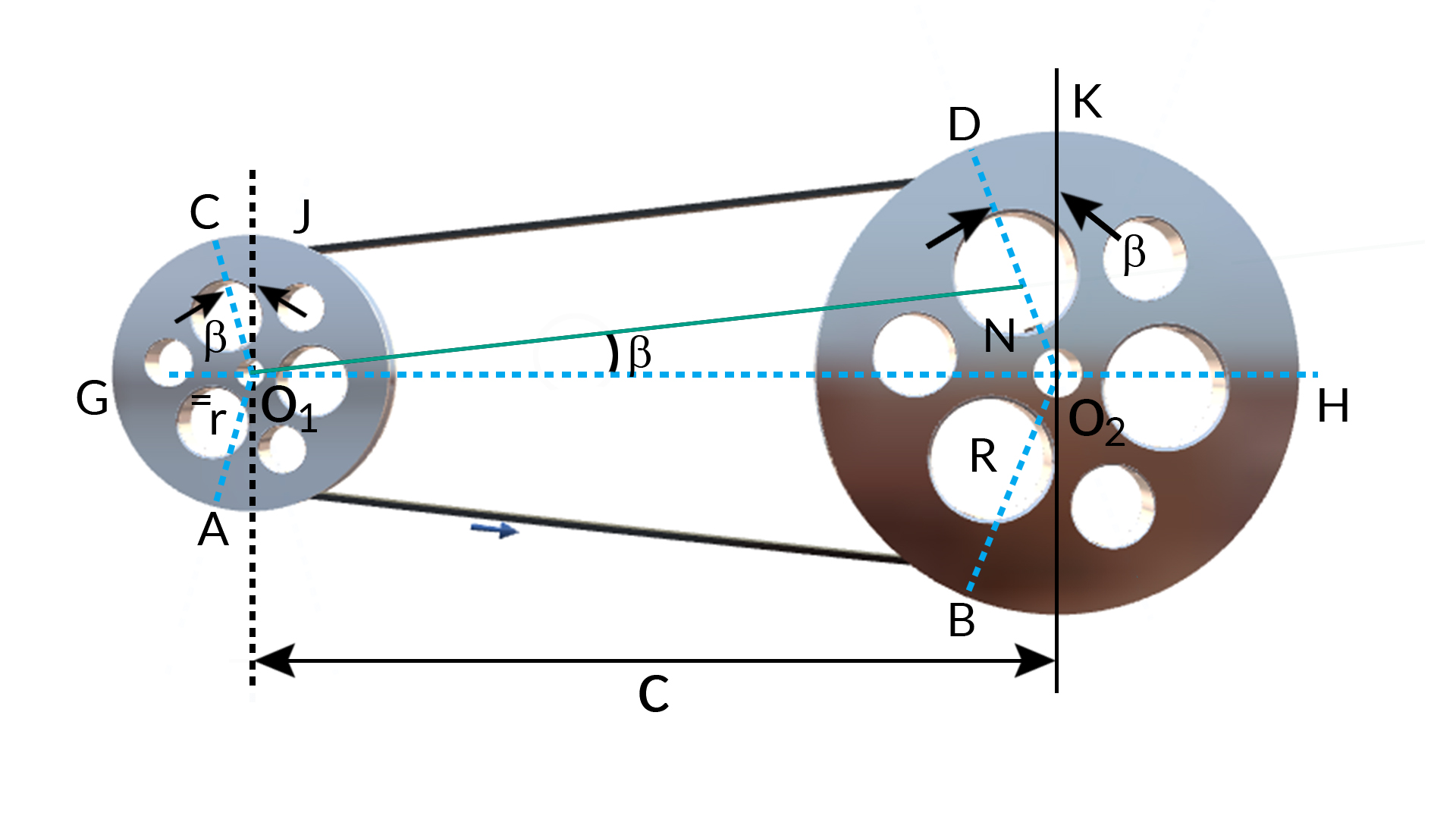
L = AB + Arc BHD + DC + Arc CGA, or  

$L= 2C +{\Pi \over 2} (D+d)+{(D-d)^2 \over 4C}$

 1.4.2 Cross belt drive

The crossed belt drive is shown in the figure. Let $O_1$ and $O_2$ be the pulley centres and AB and CD be the common tangents on the circles representing the two pulleys. The total length of the belt ‘L’ is given by
L = Belt length
C = centre of pulley shaft to centre of pulley shaft distance
D = pitch diameter of large pulley
d = pitch diameter of small pulley

$\beta$ = angle subtended by the tangents AB and CD with $O_1O_2$ 

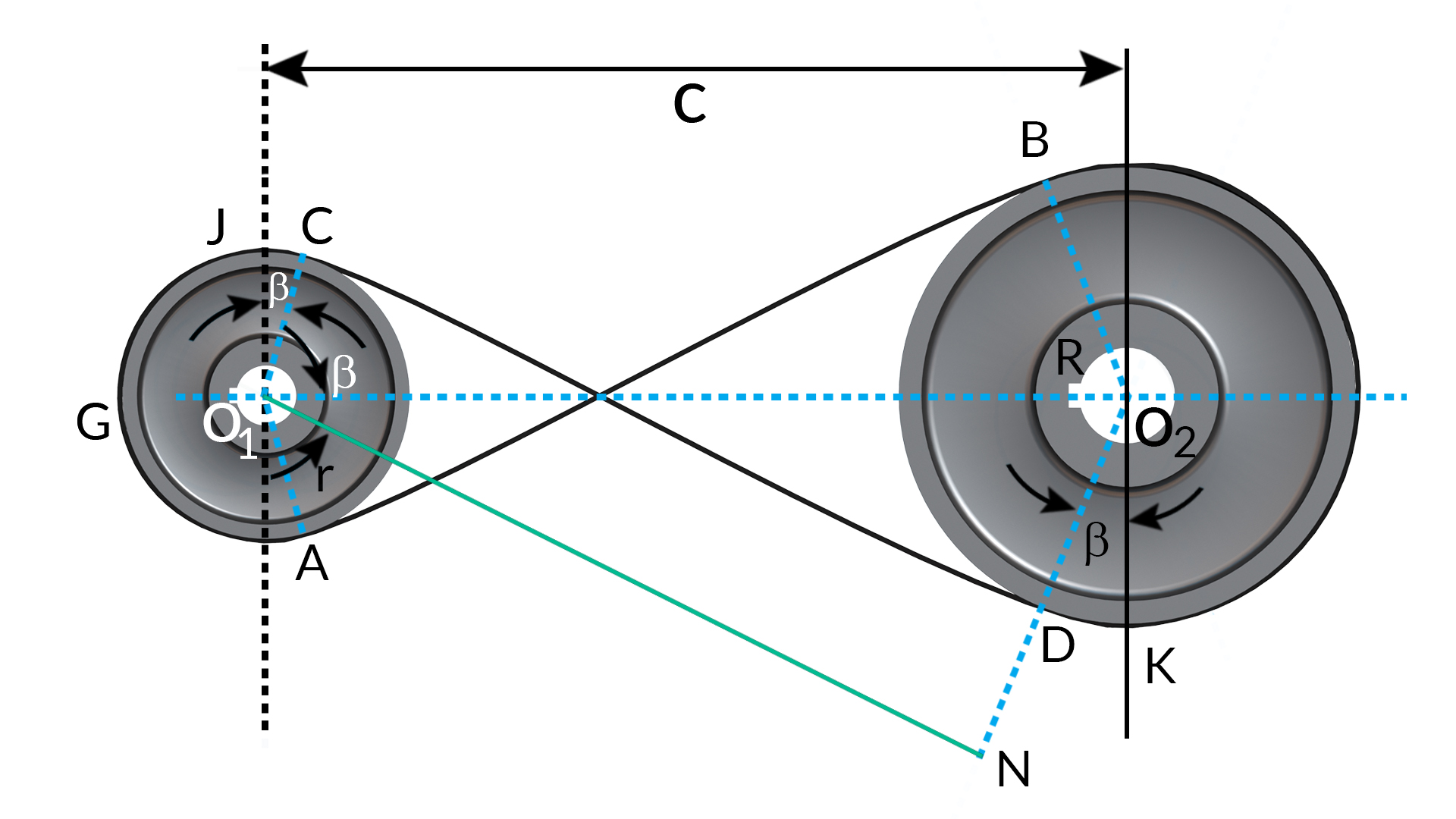
Length of the belt is 

L = Arc AGC+AB+ArcBKD+CD, or  

$L=2C +{ \Pi \over 2}(D+d) +{(D+d)^2 \over C}$

1.5 Belt Velocity Ratio

Since power transmitted by a belt drive is due to the friction, belt drive is subjected to slip and creep. Let d1 and d2 be the diameters of driving and driven pulleys, respectively. N1 and N2 be the corresponding speeds of driving and driven pulleys, respectively.

The velocity of the belt passing over the driver.

$V_1= {\pi d_1N_1 \over 60}$

If there is no slip between the belt and the pulley

$V_1=V_2 ={ \pi d_2N_2 \over 60}$, thus ${\pi d_1N_1 \over 60}={ \pi d_2N_2 \over 60}$ or ${N_1 \over N_2}={d_2 \over d_1}$

If thickness of belt is 't', and it is not negligible in comparision to the diameter,

${N_1 \over N_2}={d_2+t \over d_1+t}$

Let there be total percentage slip 'S' in the belt drive which can be taken into account as follows:

$V_2=V_1(1-{S\over 100})$ or ${\pi d_1N_1 \over 60}={ \pi d_2N_2 \over 60}(1-{S\over 100})$ and if the thickness of the belt is to be considered then,

${N_1 \over N_2}={d_2+t \over d_1+t} {1 \over (1-{S\over 100})}$, or ${N_2 \over N_1} = {(d_1+t) \over (d_2+t)} (1-{S \over 100})$

The belt moves from the tight side to the slack side and vice-versa, there is some loss of power because the length of belt continuously extends on tight side and contracts on loose side. Thus, there is relative motion between the belt and pulley due to body slip. This is known as creep.

1.6 Ratio of belt tension

A belt is able to transmit power from one shaft to another throguh the friction between the belt and pulley. Due to this riction the belt becomes tight on one side and slack on the other side. Let us determine the tensions on the belt tight and slack side

 1.6.1 Flat belt

As in the figure below
Let,
Tension on tight side – T1
Tension on slack side - T2
Angle of Lap – θ
Friction coefficient between belt and pulley - µ
Consider and infinitesimal length of the belt PQ which subtends an angle δθ at the centre fo the pulley. 

Let 'R' be the reaction between the element and the pulley. Let 'T' be tension on the slack side fo the element. i.e. at point 'P' and let '(T + δT)' be the tension on the right side of element.

The tension T and (T + δT) shall be acting tangential to the pulley and there by normal to radii OP and OQ. The fraction force shall be equal to 'µR'and its action will be to prevent slipping of the belt. The friction force will act tengentially to the pulley at the point S.

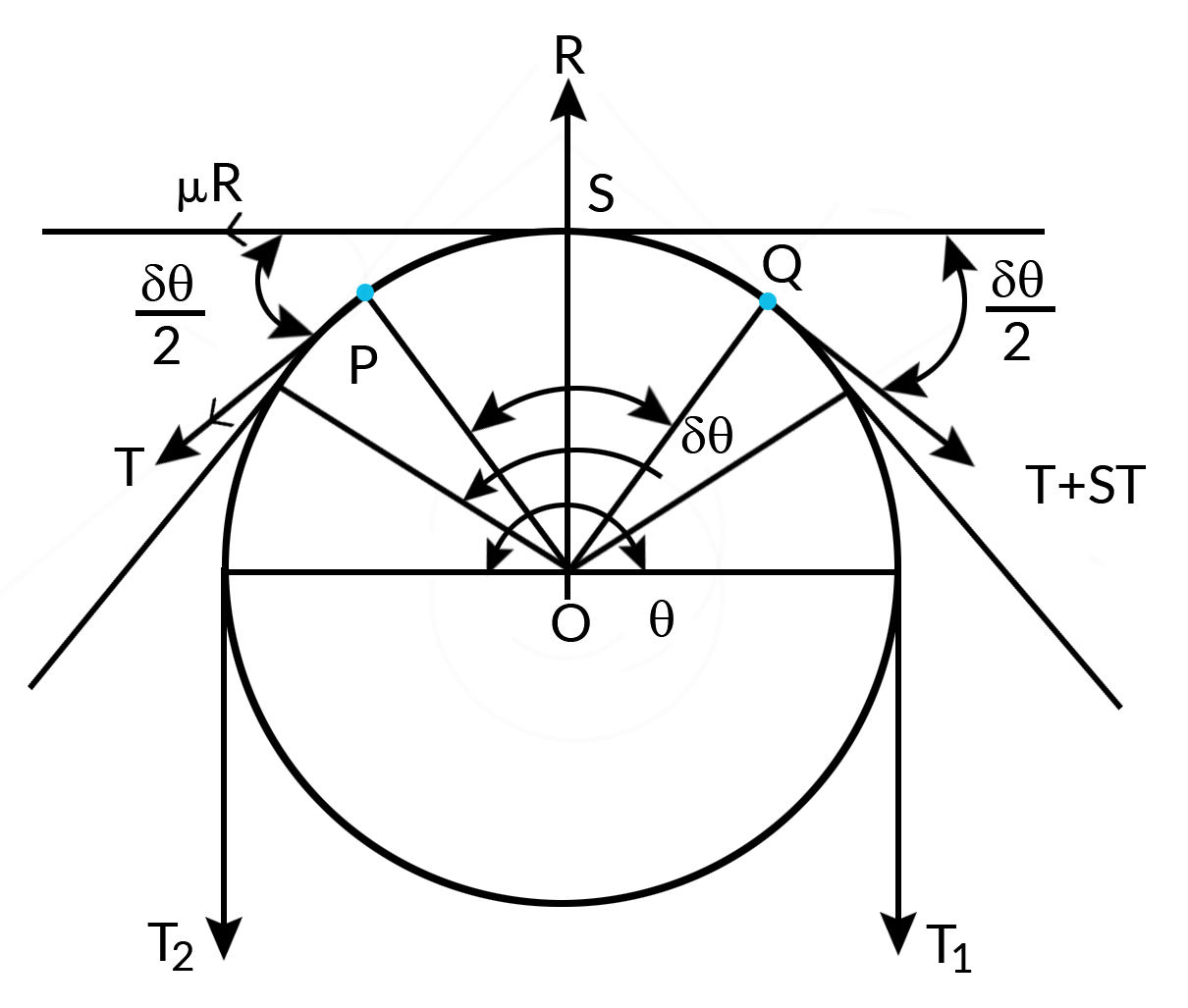
Considering equilibrium of the element at S and equating to zero.

Resolving all the forces in the tangential direction

$\mu R +T cos{\delta\theta \over 2}- (T+\delta t)cos{\delta\theta \over 2}=0$ => $\mu R = \delta tcos{\delta\theta \over 2}$

Resolving all the forces in the direction at S and equating it to zero

$R-T sin{\delta\theta \over 2}- (T+\delta t)sin{\delta\theta \over 2}=0$ or $R= (2T+\delta t)sin{\delta\theta \over 2}$

since δθ is very small, taking limits

$cos{ \delta \theta\over 2} =1 \quad and \quad sin{\delta \theta \over 2} = {\delta\theta\over2}$

therefore, $R=(2T+ \delta t){\delta \theta\over 2} \quad or \quad R=T\delta \theta +{\delta\theta . \delta t \over 2}$

Neglecting the product of two infinitesimal quantities ${\delta\theta . \delta t \over 2}$, we get $R=T\delta \theta$

Substituting the value of R and $cos{\delta\theta\over 2}$ in $\mu R = \delta tcos{\delta\theta \over 2}$

we get, $\mu T\delta\theta = \delta t =>{ \delta t \over T} =\mu \delta \theta$

Taking limit on both sides as $\delta t \quad ->0$${dt \over T }= \mu d\theta$

Integrating between limits, it becomes

$\int_{T_2}^{T_1} {dt \over T}=\int_0^\theta {\mu d \theta}$ , or $ln {T_1\over T_2} = \mu\theta$, or ${T_1 \over T_2} = e^{\mu \theta}$

 

 1.6.2 V-belt or Rope

V-belt or rope makes contact on the two sides of the groove as shown

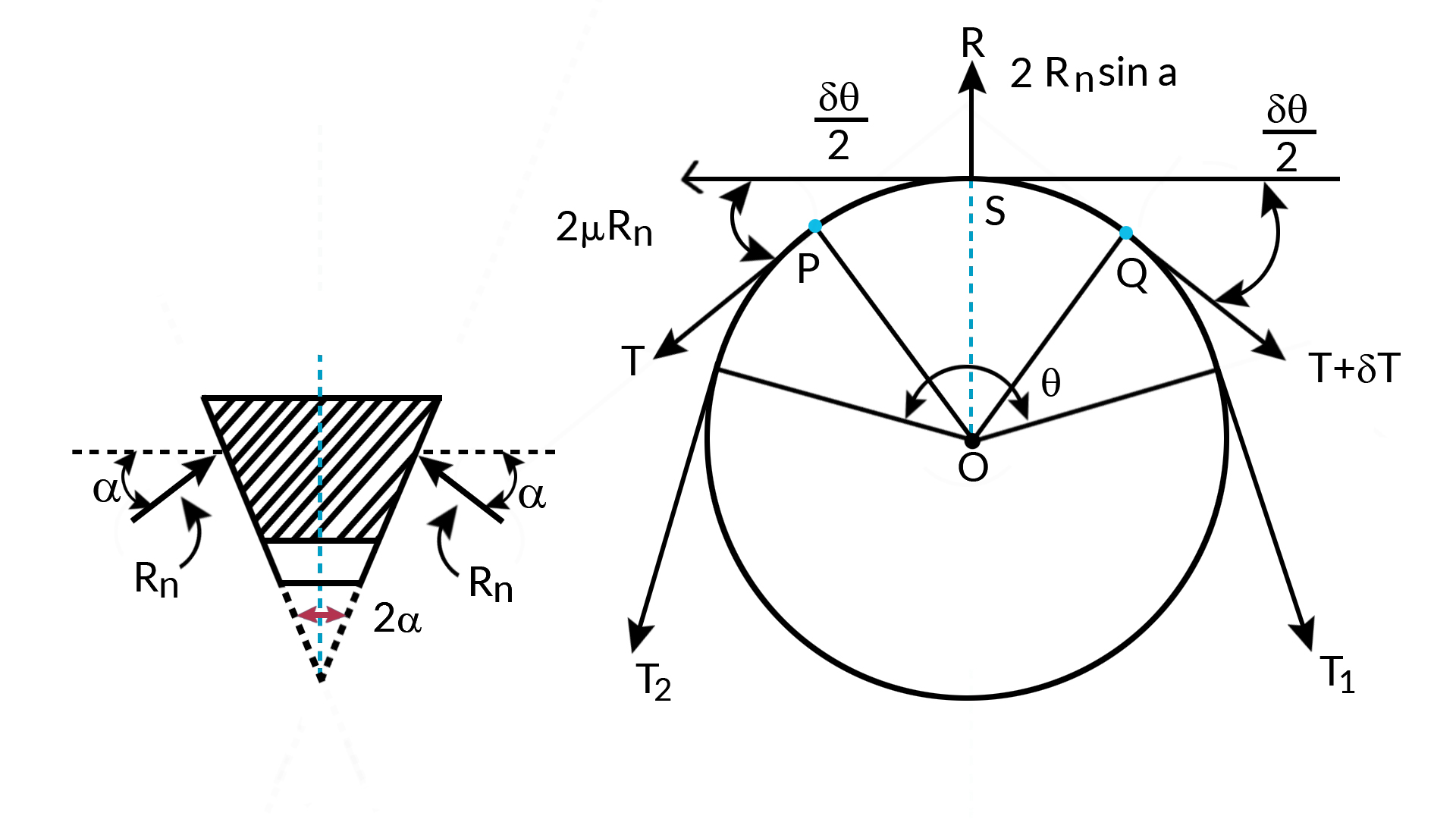
Let the reaction be 'Rn' on each of the two sides of the groove. the resultant reaction will be $2R_n sin\alpha$ at point S.
Resolving all the forces tangentially we get 

$2\mu R_n + Tcos{\delta\theta \over 2}-(T+\delta t)cos{\delta\theta \over 2} =0$ or $2\mu R_n=\delta t cos{\delta\theta \over 2}$

Resolving all the forces radially, we get $2R_nSin\alpha= TSin{\delta \theta\over 2} +(T+\delta t)sin{\delta\theta\over 2}$, or

$2R_nSin\alpha= (2T+ \delta t)sin{\delta \theta\over 2}$

since δθ is very small$sin {\delta\theta\over 2} = {\delta\theta \over 2}$

∴ $2R_nsin\alpha =T\delta\theta+\delta t.\delta\theta$

Neglecting the product of two infinitesimal quantities

$2R_nsin\alpha = T\delta \theta$ , or $R_n= {T\delta\theta \over 2sin\alpha}$

Substituting the value of Rn and using the approximitation $cos{\delta\theta\over 2} =1$, in $2\mu R_n=\delta t cos{\delta\theta \over 2}$

We get

$2 \mu {T\delta\theta \over 2sin\alpha}=\delta t =>{\delta t\over T} ={\mu\over sin\alpha} \delta\theta$

Taking the limits and integrating between limits, we get

$\int_{T_2}^{T_1} {dT\over T} = \int_0^\theta {\mu\over sin\alpha} d\theta$ => $ln({T_1\over T_2})= {\mu\over sin\alpha} \theta$, which can be further written as ${T_1\over T_2} = e^{{\mu\over sin \alpha}\theta}$

1.7 Power Transmitted by belt drive

The power transmitted by belt depends on tension on the two sides and the belt speed.
Let,

• T1 be the tension on the right side 'N'.
• T2 be the tension on the slack side in 'N' and,
• V be the speed of the belt in m/sec.

Then power Transmitted by the belt is given by

Power, $P=(T_1-T_2) V \quad watt$, or $P= T_1(1-{T_2 \over T_1}) \quad watt$, but when the belt is at the point of slipping we have , ${T_1 \over T_2} = e^{\mu \theta}$

then Power, $P= T_1 (1-e^{-\mu\theta}) \quad watts$

The maximum tension T1 depends on the capacity of the belt to withstand force. If allowable stress in the belt is ' δt' in 'Pa', i.e. N/m2, then

$T_1=\sigma_t.t.b \quad N$

Where t is the thickness of the belt in meters and b is width of the belt also in meters. This equation can also be used to determine 'b' for given power and speed.

1.8 Tension due to Centrifugal Forces

The belt has mass and it rotates along with the pulley then it is subjected to centrifugal forces. If we assume that no power is being transmitted and pulleys are rotating, the centrifugal force will tend to pull the belt as shown and, thereby, a tension in the belt is called centrifugal tension will be introduced.

Let 'Tc' be the centrifugal tension due to centrifugal force.
Let us consider a samll element which subtends an angle δθ at the center of the pulley.
Let 'm' be the mass of the belt per unit length of the belt in 'kg/m'.
The centrifugal force 'Fc' on the element will be given by 

$F_c=(r\delta \theta m) {V^2\over r}$

where V is the speed of the belt in m/sec. and r is the radius of pulley in 'm'.
Resolving the forces on the element normal to the tangent

$F_c-2T_c sin{\delta\theta\over 2} =0$

since δθ is very small

∴ $sin{\delta\theta \over 2}={\delta\theta \over 2}$
or,

$F_c-2T_c {\delta\theta\over 2} =0$

or,

$F_c=T_c \delta\theta$,  Substituting for FC in $F_c=(r\delta \theta m) {V^2\over r}$, we get

$T_c\delta\theta=(r.m.\delta\theta){V^2\over r} => T_c= mV^2$

Therefore consideing the effect of the centrifugal tension, the belt tension on the right side when power is transmitted is given by 
Tension of right side $T_t=T_1+T_c$ and the tension on the slack side $T_s=T_2+T_c$.
The centrifugal tension has an effect on the power transmitted because maximum tension can be only $T_t$ which is

$T_t=\sigma_t.t.b$, therefore $T_1=\sigma_t.t.b-mV^2$

 

1.9 Initial Tension

When belt is mounted on the pulley some amount of initial tension say 'T0' is provided in the belt, otherwise power transmission is not possible because of loose belt can not sustain difference in the tension and no power can be transmitted. When the drive is stationary the total tension on both sides will be '2T0'. When belt drive is transmitting power the total tension on both sides will be 'T1 + T2', where T1 is tension on right side and T2 is tension on the slack side.
If the effect of centrifugal tension is neglected .

$2T_0=T_1+T_2$ or, $T_0={T_1+T_2\over 2}$

If the effect of centrifugal tension is considered, then

$2T_0=T_t+T_s =T_1+T_2+2T_c$ or, $T_0={T_1+T_2 \over 2}+T_c$

 

1.10 Maximum Power Transmitted

The power transmitted depends on the tension 'T1', angle of lap θ, coefficient of friction 'μ' and the belt speed 'V'. For a driven belt drive, the maximum tension (Tt), angle of lap and coefficient of friction shall remain constant provided that

1. the tension on right side, i.e. maximum tension should be equal to the maximum permissible value for the belt,and
2. the belt should be at the point of slipping

Therefore, Power $P=T_1(1-e^{-\mu\theta}) V$

since, $T_1=T_t+T_c$
or,

$P=(T_t-T_c)(1-e^{-\mu\theta})V$

or,

$P=(T_t-mV^2)(1-e^{-\mu\theta})V$, for mximum power transmitted, we differentiate the expression and equate to 0. Hence

${dP\over dV} =(T_t-3mV^2)(1-e^{-\mu\theta})=0$ ,Thus 

$T_t-3T_c=o \quad or\quad T_c={T_t \over 3}$, also  $T_c =mV^2$,

therefore $V=\sqrt {T_t \over 3m}$
At the belt speed given by the above equation. the power transmited by the belt drive shall be maximum.